Books
- Cracking the Coding Interview: 189 Programming Questions and Solutions
- Grokking Algorithms: An Illustrated Guide for Programmers and Other Curious People
- Introduction to Algorithms - Thomas H Cormen
- Learning JavaScript Data Structures and Algorithms: Write complex and powerful JavaScript code using the latest ECMAScript, 3rd Edition - Loiane Groner
Design Patterns
YouTube
- Crash Course Computer Science
- Linguagem C Programação Descomplicada
- 5 Simple Steps for Solving Any Recursive Problem
- Como Reinventar o Computador do Zero
Sites
GitHub Repositories
- The Algorithms - Open Source resource for learning Data Structures & Algorithms and their implementation in any Programming Language
- Javascript Datastructures Algorithms - Loiane Groner
- JavaScript Algorithms
- https://github.com/antlr/grammars-v4
- Javascript Questions and their explanations
Entropy & Information Theory
Code Training
- Project Euler
- HackerRank
- LeetCode
- Edabit
- Exercism
- AlgoExpert.io
- URI Online Judge
- 7 Days Of Code
- 100 days of code
KhanAcademy
Data Structures Visualization
Programming Paradigms
1. Procedural Paradigm
- Definition: Focuses on procedures or routines (functions) to operate on data.
- Main Feature: Code organized into functions that execute a sequence of instructions.
Example in C:
#include <stdio.h>
void sayHello() {
printf("Hello, World!\n");
}
int main() {
sayHello();
return 0;
}
2. Imperative Paradigm
- Definition: Describes computation as a series of instructions that change the state of the program.
- Main Feature: Emphasizes how to perform tasks (step by step).
JavaScript Example:
let total = 0;
for (let i = 1; i <= 10; i++) {
total += i;
}
console.log(total); // 55
3. Functional Paradigm
- Definition: It is based on the evaluation of mathematical functions and avoids the use of mutable states.
- Main Feature: Pure functions and immutability.
Elixir Example:
defmodule Math do
def sum(a, b) do
a + b
end
end
IO.puts Math.sum(1, 2) # 3
4. Object-Oriented Paradigm (OOP)
- Definition: It is based on objects that contain data and methods to operate on that data.
- Main Feature: Encapsulation, inheritance, polymorphism.
Example in Python:
class Animal:
def __init__(self, name):
self.name = name
def speak(self):
pass
class Dog(Animal):
def speak(self):
return f"{self.name} says Woof!"
dog = Dog("Buddy")
print(dog.speak()) # Buddy says Woof!
5. Declarative Paradigm
- Definition: Describes what the program should do, not how to do it.
- Main Feature: Specifies the desired result without detailing the steps.
Example in SQL:
SELECT * FROM products WHERE price > 100;
6. Logical Paradigm
- Definition: Relies on rules and logic to derive conclusions from facts.
- Main Feature: Uses formal logic to express relationships.
Example in Prolog:
parent(john, mary).
parent(mary, susan).
grandparent(X, Y) :- parent(X, Z), parent(Z, Y).
7. Structured Paradigm
- Definition: Emphasizes dividing the program into modules or blocks.
- Main Feature: Uses control structures such as loops and conditionals.
Example in TypeScript:
function factorial(n: number): number {
if (n <= 1) {
return 1;
}
return n * factorial(n - 1);
}
console.log(factorial(5)); // 120
Summary:
- Procedural: Functions and procedures (C).
- Imperative: Step-by-step (JavaScript).
- Functional: Pure functions, without mutable states (Elixir).
- Object-oriented (OOP): Objects and methods (Python).
- Declarative: Focus on what to do, not how (SQL).
- Logical: Rules and formal logic (Prolog).
- Structured: Blocking and flow control (TypeScript).
These paradigms help to structure and organize code in different ways, each with its benefits and best applications.
P vs NP Problems
-
Imagine you have a super hard puzzle to solve. Now, you want to know if there is a quick way to solve this puzzle, like some magic or special formula that solves it instantly. That would be awesome, right?
-
The P vs NP problem is like a big question about these types of puzzles. “P” is like a puzzle box where we can solve the problems quickly, in a time that doesn’t increase much as the puzzle gets bigger. “NP”, on the other hand, is like a box where, if someone shows you the solution, you can check if it’s correct quickly, but finding that solution can be very difficult.
-
The big question is: can all the problems that we can check quickly (NP) also be solved quickly (P)? If so, that would be awesome because all these hard puzzles would have quick solutions like magic. But so far, no one has been able to prove or disprove it. It’s like we’re all trying to figure out if there is a magic formula to solve these hard puzzles or if we’ll always have to solve them patiently, piece by piece. It’s a giant mystery that computer scientists are still trying to unravel!
Source: https://www.youtube.com/watch?v=pQsdygaYcE4
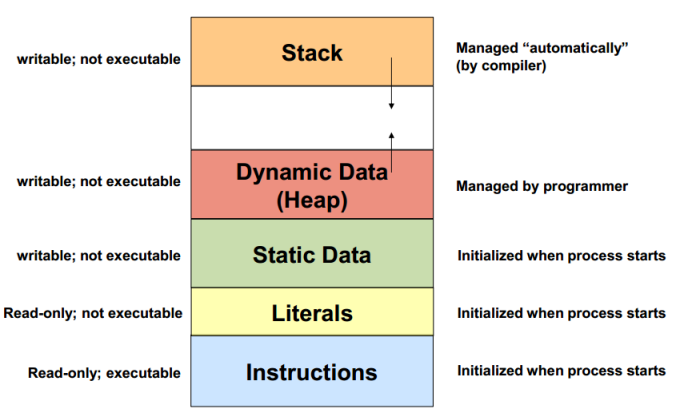
Stack vs Heap
Let’s imagine that your computer’s memory is like a bookshelf with several shelves. When you need to store something, you can put it on one of these shelves in two different ways: stack and heap.
Stack
-
Organization: The stack is like a stack of plates, where you put one plate on top of another. The last plate to be put on is the first to be removed.
-
Speed: The stack is very fast because the plates (data) are accessed in a specific order (LIFO - Last In, First Out).
-
Fixed Size: The stack has a fixed size. This means that you can only stack a limited number of plates before the stack becomes full.
-
Automatic Management: When you put a plate (variable) on the stack, it is automatically removed when it is no longer needed.
Heap
-
Organization: The heap is like a big pile of toys lying around. You can pick up and put toys anywhere.
-
Speed: The heap is slower than the stack because you may need to search for free space to put a new toy (data).
-
Variable Size: The heap can grow and shrink as needed, so you can add lots of toys (data) without worrying too much about space.
-
Manual Management: When you put a toy in the heap, you need to remember to take it out when you’re done using it. If you forget, memory can get messed up (memory leaks).
Example in C
#include <stdio.h>
#include <stdlib.h>
// Function using the stack
void stackExample() {
int stackVar = 10; // The variable is stored in the stack
printf("Variable value in the stack: %d\n", stackVar);
}
// Function using the heap
void heapExample() {
int *heapVar = (int *)malloc(sizeof(int)); // The variable is stored in the heap
if (heapVar != NULL) {
*heapVar = 20;
printf("Variable value in the heap: %d\n", *heapVar);
free(heapVar); // Remember to free the memory!
}
}
int main() {
stackExample();
heapExample();
return 0;
}
Code Explanation
- Stack Example:
- int stackVar = 10; places the variable stackVar on the stack.
- When stackExample() finishes, stackVar is automatically removed from memory.
- Heap Example:
- int _heapVar = (int _)malloc(sizeof(int)); places the variable heapVar on the heap.
- *heapVar = 20; assigns the value 20 to the allocated space in the heap.
- free(heapVar); frees the heap memory to prevent leaks.
Dinamic Programming
- Let’s imagine that you are in a big maze and need to find the way out. In this maze, you can choose several different paths, but some paths may lead you to dead ends or be longer than others.
- Dynamic programming is like a superpower that helps you solve problems faster and more efficiently by remembering the solutions to subproblems that you have already solved before.
- Instead of solving the same problem several times, you save the answers to smaller parts of the problem in a kind of notebook. That way, when you come across a similar problem, you don’t have to solve it all over again – you can just look in the notebook to find the answer.
- Let’s use a simple example: imagine that you want to find out how many different ways you can climb a staircase with 10 steps, whether you can climb 1 or 2 steps at a time.
- If you only have 1 step, there is only one way to climb (1 step at a time).
- If you have 2 steps, you can climb them in two ways: 1 step + 1 step, or 2 steps at once.
- For more steps, you can think of it like this:
- To get to the 3rd step, you can either come from the 2nd step (and climb 1) or from the 1st step (and climb 2).
- This means that the ways to get to the 3rd step are the sum of the ways to get to the 2nd step and the ways to get to the 1st step. So, if you write down this information:
- 1 step: 1 way
- 2 steps: 2 ways
- 3 steps: 1 (from the 2nd step) + 2 (from the 1st step) = 3 ways
- And so on…
- This is dynamic programming: solving a big problem (how many ways to climb 10 steps) by breaking it down into smaller problems (how many ways to climb 1, 2, 3… steps) and remembering the answers to these smaller problems to avoid having to solve everything from scratch again.
- In short, dynamic programming is a technique that helps us solve complex problems efficiently by remembering the solutions to the smaller problems so we don’t have to solve the same thing more than once.
- Algorithm Example: Tower Of Hanoi
function hanoiTower(
n: number,
source: string,
auxiliary: string,
destination: string
): void {
if (n === 1) {
console.log(`Move disk 1 from ${source} to ${destination}`);
return;
}
hanoiTower(n - 1, source, destination, auxiliary);
console.log(`Move disk ${n} from ${source} to ${destination}`);
hanoiTower(n - 1, auxiliary, source, destination);
}
hanoiTower(5, "A", "B", "C");
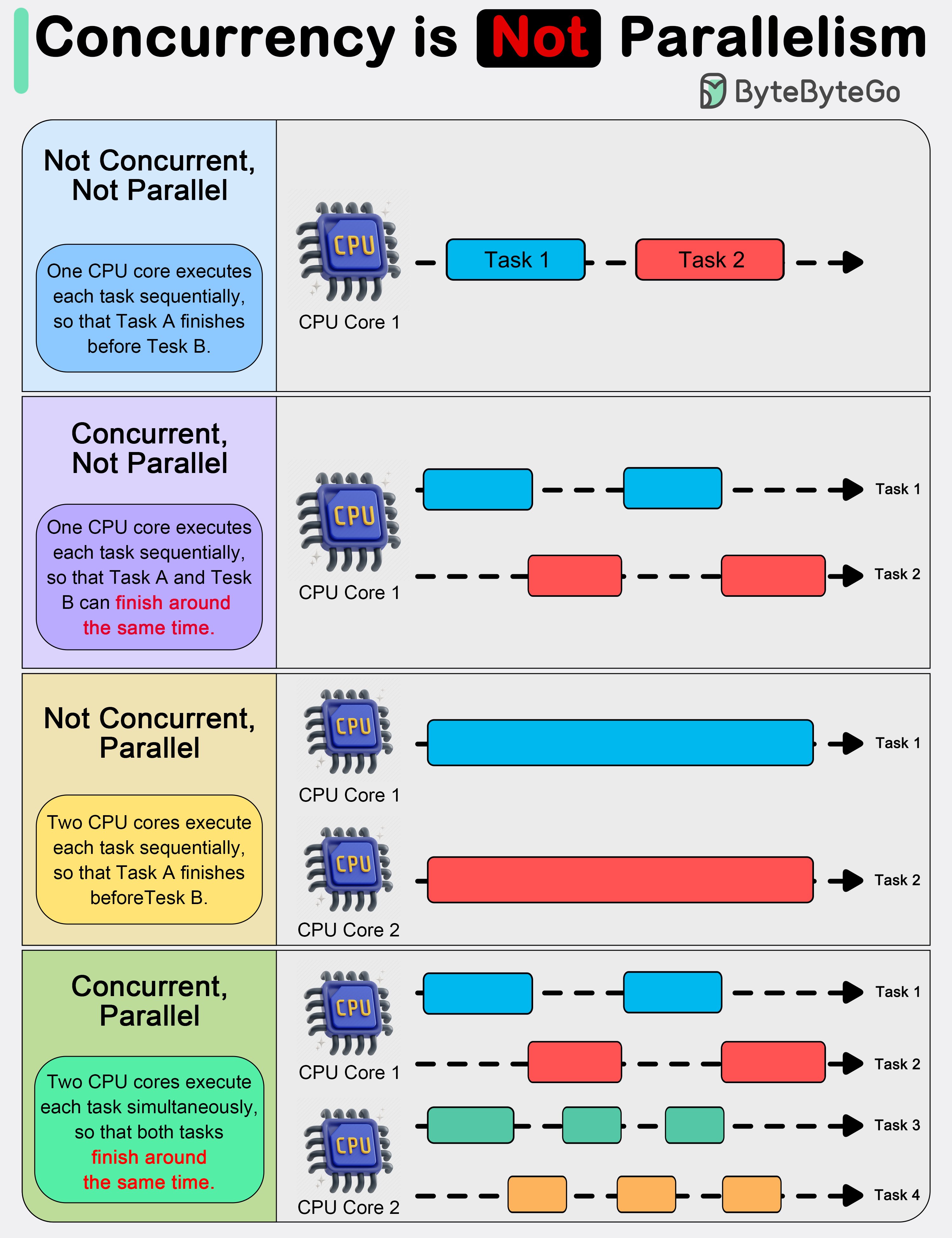
Concurrency vs Parallelism
- As Rob Pike (one of the creators of GoLang) stated:
- “Concurrency is about 𝐝𝐞𝐚𝐥𝐢𝐧𝐠 𝐰𝐢𝐭𝐡 lots of things at once.
- Parallelism is about 𝐝𝐨𝐢𝐧𝐠 lots of things at once.”
- This distinction emphasizes that concurrency is more about the 𝐝𝐞𝐬𝐢𝐠𝐧 of a program, while parallelism is about the 𝐞𝐱𝐞𝐜𝐮𝐭𝐢𝐨𝐧.
- Concurrency is about dealing with multiple things at once. It involves structuring a program to handle multiple tasks simultaneously, where the tasks can start, run, and complete in overlapping time periods, but not necessarily at the same instant.
- Concurrency is about the composition of independently executing processes and describes a program’s ability to manage multiple tasks by making progress on them without necessarily completing one before it starts another.
- Parallelism, on the other hand, refers to the simultaneous execution of multiple computations. It is the technique of running two or more tasks or computations at the same time, utilizing multiple processors or cores within a computer to perform several operations concurrently.
- Parallelism requires hardware with multiple processing units, and its primary goal is to increase the throughput and computational speed of a system.
- In practical terms, concurrency enables a program to remain responsive to input, perform background tasks, and handle multiple operations in a seemingly simultaneous manner, even on a single-core processor.
- It’s particularly useful in I/O-bound and high-latency operations where programs need to wait for external events, such as file, network, or user interactions.
- Parallelism, with its ability to perform multiple operations at the same time, is crucial in CPU-bound tasks where computational speed and throughput are the bottlenecks.
- Applications that require heavy mathematical computations, data analysis, image processing, and real-time processing can significantly benefit from parallel execution.
Mutex (Mutual Exclusion)
A mutex is a way to ensure that only one thread or process can access a shared resource at a time. It’s like a key you need to enter a room; if someone is already in the room and has the key, you need to wait.
class Mutex {
private locked = false;
async lock() {
while (this.locked) {
await new Promise(resolve => setTimeout(resolve, 10));
}
this.locked = true;
}
unlock() {
this.locked = false;
}
}
const mutex = new Mutex();
async function criticalSection() {
await mutex.lock();
try {
// Code that accesses the shared resource
console.log("Resource accessed");
} finally {
mutex.unlock();
}
}
criticalSection();
criticalSection();
Semaphore
A semaphore is a variable used to control access to multiple resources. It can be incremented and decremented and has a maximum limit.
class Semaphore {
private counter: number;
private waiting: (() => void)[] = [];
constructor(counter: number) {
this.counter = counter;
}
async wait() {
if (this.counter > 0) {
this.counter--;
} else {
await new Promise<void>(resolve => this.waiting.push(resolve));
}
}
signal() {
if (this.waiting.length > 0) {
const resolve = this.waiting.shift();
resolve?.();
} else {
this.counter++;
}
}
}
const semaphore = new Semaphore(2);
async function accessResource() {
await semaphore.wait();
try {
// Code that accesses shared resources
console.log("Resource accessed");
} finally {
semaphore.signal();
}
}
accessResource();
accessResource();
accessResource();
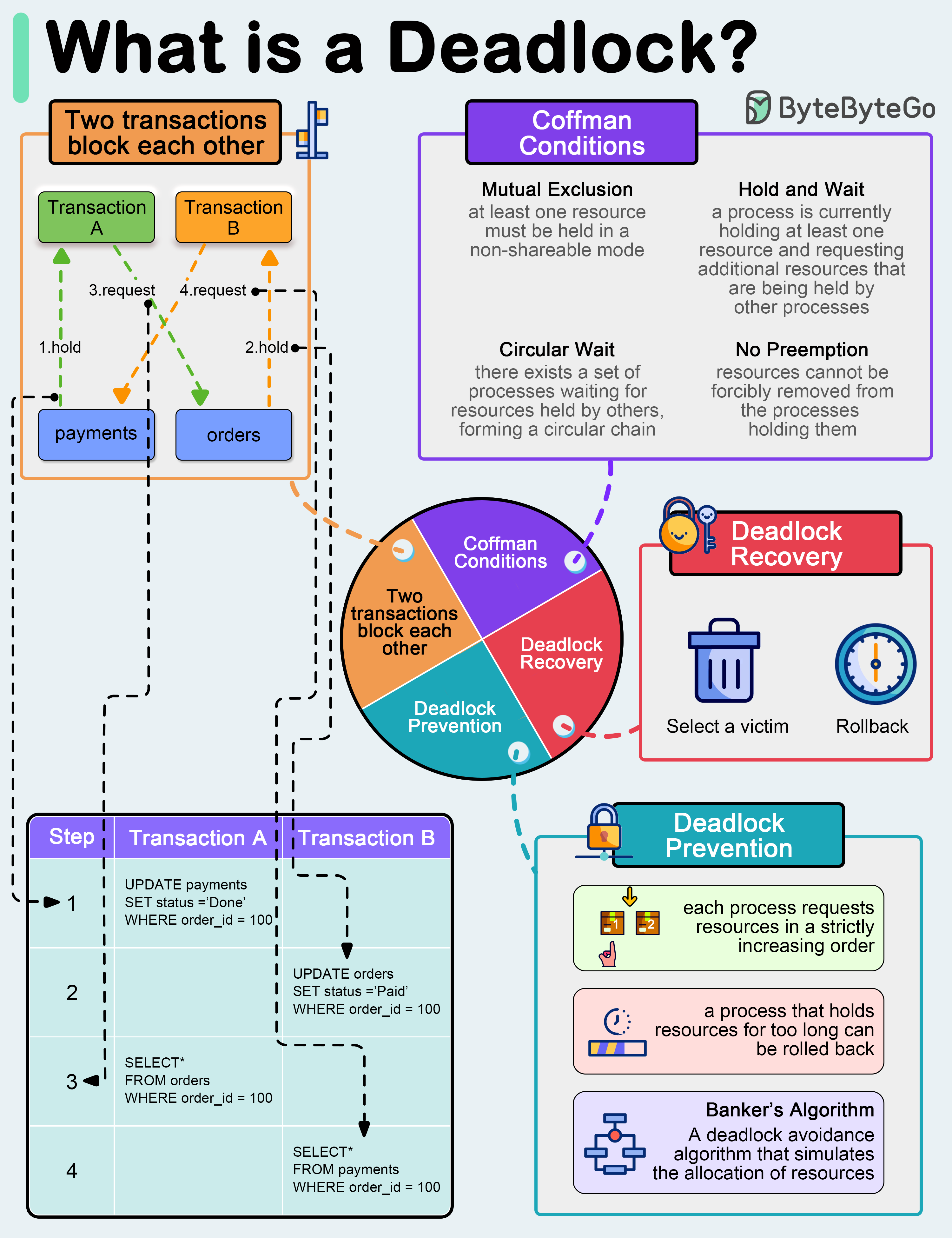
Deadlock
A deadlock happens when two or more threads get stuck waiting for each other to release resources, and neither can continue.
const mutexA = new Mutex();
const mutexB = new Mutex();
async function task1() {
await mutexA.lock();
console.log("Task 1: Locked A");
await new Promise(resolve => setTimeout(resolve, 100)); // Simulate some operation
await mutexB.lock();
console.log("Task 1: Locked B");
mutexB.unlock();
mutexA.unlock();
}
async function task2() {
await mutexB.lock();
console.log("Task 2: Locked B");
await new Promise(resolve => setTimeout(resolve, 100)); // Simulate some operation
await mutexA.lock();
console.log("Task 2: Locked A");
mutexA.unlock();
mutexB.unlock();
}
task1();
task2();
Race Condition
A race condition occurs when the outcome of the software depends on the sequence or timing of uncontrolled events. This usually occurs when two or more threads or processes access and modify a shared resource at the same time.
let counter = 0;
async function increment() {
const temp = counter;
await new Promise(resolve => setTimeout(resolve, 100)); // Simulate some operation
counter = temp + 1;
}
increment();
increment();
increment();
setTimeout(() => {
console.log(counter); // May not be 3 due to race condition
}, 500);
To avoid race conditions, we use mutexes or other forms of synchronization.
Summary:
- Mutex: Ensures exclusive access to a resource.
- Semaphore: Controls access to multiple resources.
- Deadlock: When threads are stuck waiting for each other.
- Race Condition: When the result depends on the sequence/timing of events.
These concepts are fundamental to managing concurrency in multithreaded systems.
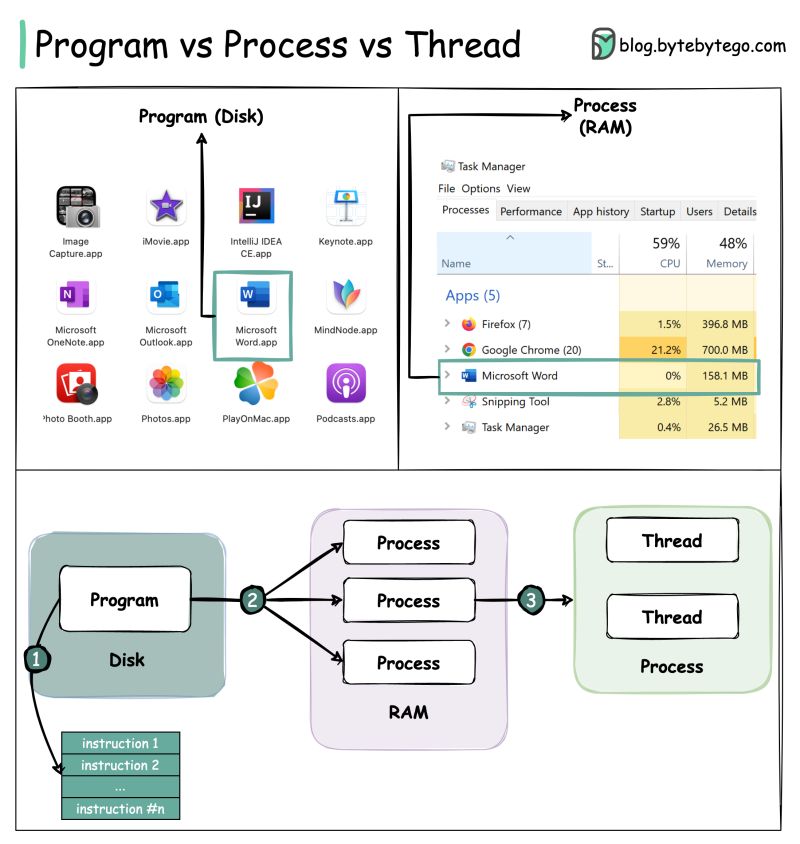
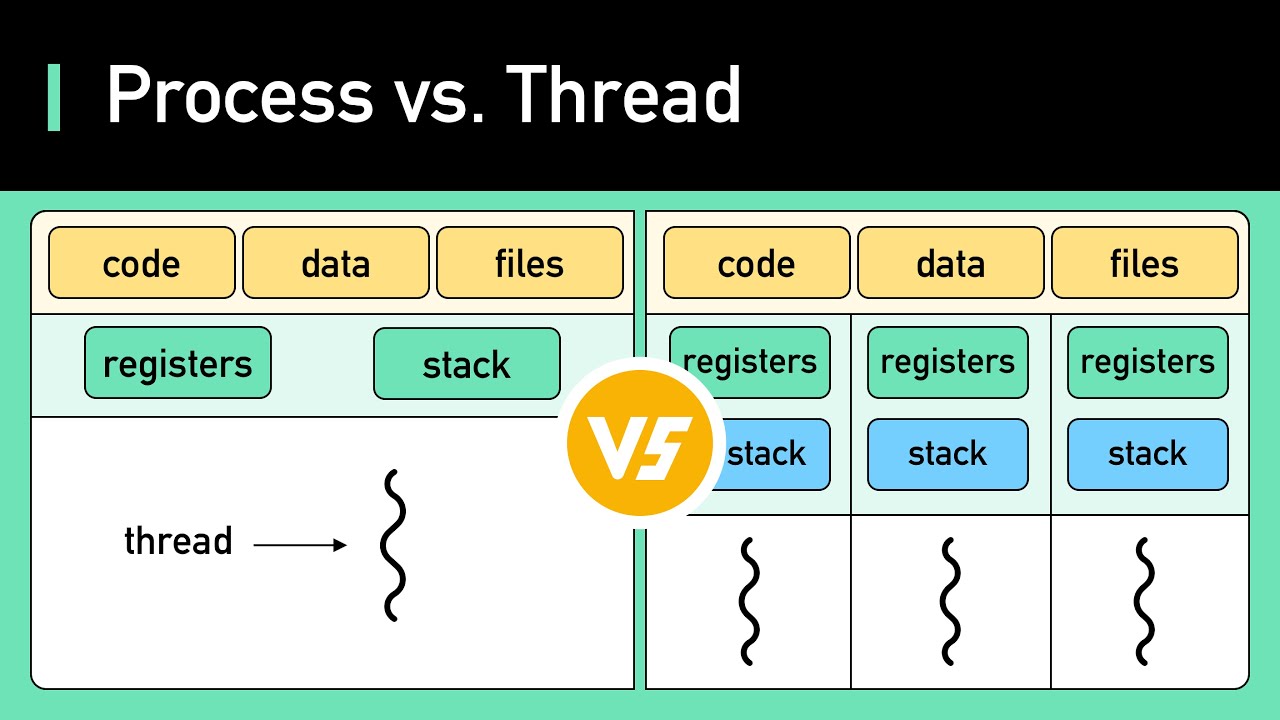
Process vs Threads
Processes:
- Think of a process as a program that you open on your computer. For example, when you open a game or a web browser, each of them is a process.
- Each process has its own “toy box” (memory) that it uses to store things (data) while it is running. These boxes are separate, so one process cannot touch another’s toys.
Threads:
- Within a process, we can have several threads. Think of threads as helpers inside this “toy box” (process).
- Threads can share the toys (data) in the same box, which means they can work together faster, but they also need to be careful not to mess things up.
Main differences
- Isolation: Processes are like separate boxes, and each one has its own toys. Threads share the same box and toys.
- Communication: Processes need special ways to talk to each other, like using a telephone. Threads can talk directly to each other because they are in the same box.
- Cost: Creating a new process is like buying a new box of toys — it takes more time and uses more energy. Creating a new thread is like getting another helper to play in the same box — it’s faster and easier.
Usage examples with TypeScript and Node.js
Process Example: Let’s say you want to run a large script that will take a long time. Instead of doing it in the same program, you can create a new process for it.
import { fork } from "child_process";
// Create a new process to run the script 'longTask.ts'
const newProcess = fork("longTask.ts");
newProcess.on("message", message => {
console.log("Message from child process:", message);
});
newProcess.send("Start heavy task");
Thread Example: If you want to do several things at the same time within the same program, you can use threads (in Node.js, we use “worker threads”).
import { Worker } from "worker_threads";
// Function that creates a new worker
function runService(workerData: any) {
return new Promise((resolve, reject) => {
const worker = new Worker("./workerTask.js", { workerData });
worker.on("message", resolve);
worker.on("error", reject);
worker.on("exit", code => {
if (code !== 0) {
reject(new Error(`Worker stopped with code ${code}`));
}
});
});
}
// Call the worker with the necessary data
runService("Data for the worker")
.then(result => {
console.log("Worker result:", result);
})
.catch(err => {
console.error(err);
});
When to use each
- Processes are great when you need to run very heavy or separate tasks that shouldn’t interfere with each other.
- Threads are better for tasks that need to work together and share data quickly.
So, processes and threads help you do more things at the same time in your program, but in different ways. Processes are more isolated and safe, while threads are faster and more collaborative.
Memory Leaks
Imagine you’re playing a block game, where you build things with toy blocks. Each time you pick up a block, you have to return it to the box when you’re done using it. A memory leak is like you pick up blocks from the box, but never return them. Over time, the box becomes empty and you’re left with no blocks to play with, even though there are still plenty of blocks scattered around the floor.
In programming, a memory leak happens when a program reserves memory to use (like picking up blocks from the box), but doesn’t release that memory when it’s done (like not returning the blocks). This causes the computer’s available memory to gradually decrease, which can cause the program or even the computer to crash.
Examples in Different Languages
Python
Python usually manages memory for you, but you can get memory leaks by keeping unnecessary references to objects.
class Block:
def __init__(self):
self.data = [0] * 1000000 # too much data, too much memory!
def create_blocks():
blocks = []
while True: # infinite loop!
blocks.append(Block()) # we keep creating blocks and never freeing them
create_blocks()
TypeScript
In TypeScript, a memory leak can happen when you create objects and never remove references to them.
class Block {
data: number[];
constructor() {
this.data = new Array(1000000).fill(0); // too much data, too much memory!
}
}
const blocks: Block[] = [];
function createBlocks() {
setInterval(() => {
blocks.push(new Block()); // we keep creating blocks and never free them
}, 1000);
}
createBlocks();
C
In C, you have to manually manage memory allocation and freeing.
#include <stdlib.h>
typedef struct {
int *data;
} Block;
void create_blocks() {
while (1) { // infinite loop!
Block *block = (Block *)malloc(sizeof(Block));
block->data = (int *)malloc(1000000 * sizeof(int)); // lots of memory allocated
// we never free the memory allocated with free()
}
}
int main() {
create_blocks();
return 0;
}
Rust
Rust helps prevent memory leaks with its memory management system, but they can still happen in certain cases.
struct Block {
data: Vec<i32>,
}
fn create_blocks() {
let mut blocks = Vec::new();
loop {
let block = Block { data: vec![0; 1_000_000] }; // lots of memory allocated
blocks.push(block); // we keep creating blocks and never freeing them
}
}
fn main() {
create_blocks();
}
In short
A memory leak is like taking toy blocks and never putting them back in the box. In programming, it is reserving memory and never freeing it. This can leave the computer with no available memory, causing programs and the computer itself to crash.
What are Pointers?
Imagine that you have a treasure hidden on a map. The pointer is like an “arrow” that points to the location of the treasure on the map. In programming, a pointer is something that points to a place in the computer’s memory where a value is stored.
Passing by Value vs. Passing by Reference
Passing by Value
Imagine that you have a toy and you lend it to a friend. Instead of giving the actual toy, you give an exact copy of the toy. Now, if your friend breaks the toy, your actual toy is still safe.
In programming, passing by value means giving a copy of the data to a function. If the function modifies the copy, the original data remains unchanged.
Passing by Reference
Now, imagine that you lend your actual toy to your friend. If he breaks the toy, your actual toy will be broken.
In programming, passing by reference means giving the location (or address) of the data to a function. If the function modifies the data, the original data is changed.
Examples in TypeScript and C
TypeScript
Passing by Value
In TypeScript, primitive types (like numbers) are passed by value.
function changeValue(x: number): void {
x = 10;
console.log("Inside function:", x);
}
let originalValue = 5;
console.log("Before function:", originalValue);
changeValue(originalValue);
console.log("After function:", originalValue);
In this example, originalValue is not changed because a copy of originalValue is passed to the changeValue function.
Passing by Reference
In TypeScript, objects are passed by reference.
function changeObject(obj: { value: number }): void {
obj.value = 10;
console.log("Inside function:", obj.value);
}
let originalObject = { value: 5 };
console.log("Before function:", originalObject.value);
changeObject(originalObject);
console.log("After function:", originalObject.value);
In this example, originalObject is changed because the changeObject function receives the object reference and directly modifies the value.
C
Passing by Value
In C, primitive types (such as integers) are passed by value.
#include <stdio.h>
void changeValue(int x) {
x = 10;
printf("Inside function: %d\n", x);
}
int main() {
int originalValue = 5;
printf("Before function: %d\n", originalValue);
changeValue(originalValue);
printf("After function: %d\n", originalValue);
return 0;
}
In this example, originalValue is not changed because a copy of originalValue is passed to the changeValue function.
Passing by Reference
In C, you can pass the reference (address) of a variable using pointers.
#include <stdio.h>
void changeValue(int *x) {
*x = 10;
printf("Inside function: %d\n", *x);
}
int main() {
int originalValue = 5;
printf("Before function: %d\n", originalValue);
changeValue(&originalValue);
printf("After function: %d\n", originalValue);
return 0;
}
In this example, originalValue is changed because the changeValue function receives a pointer to originalValue and directly modifies the value using the pointer.
Summary
- Pointers are like arrows that point to places in memory where data is stored.
- Passing by Value means giving a copy of the data to a function.
- Passing by Reference means giving the location of the data to a function, allowing the function to modify the original data.
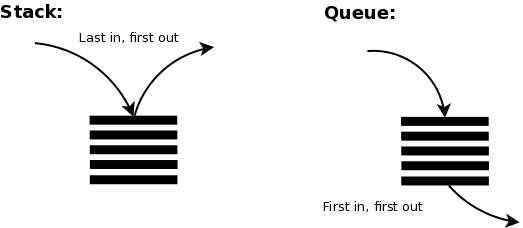
Stack vs Queue
- QUEUE
- FIFO
- First In, First Out
- FIFO
- STACK
- LIFO
- Last In, First Out
- LIFO
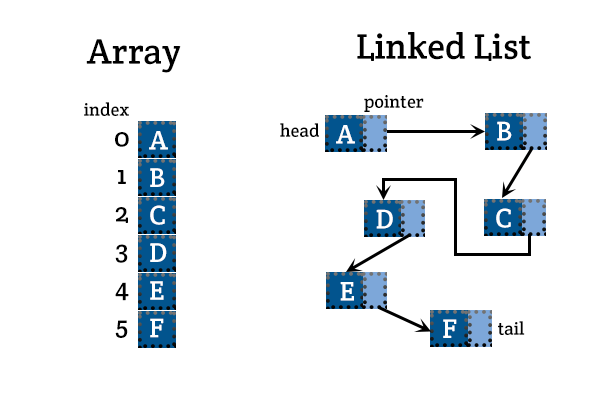
Arrays vs Lists
-
Arrays
- Structure:
- Fixed Size: Arrays have a fixed size determined at the time of creation.
- Contiguous Memory: Elements are stored in contiguous memory locations.
- Access Time:
- Random Access: Arrays allow O(1) time complexity for accessing elements by index.
- Insertion and Deletion:
- Expensive Operations: Inserting or deleting elements (except at the end) requires shifting elements, leading to O(n) time complexity.
- Memory Utilization:
- Static Allocation: Memory is allocated at the time of array creation and cannot be resized.
- Cache Performance:
- Better Cache Locality: Due to contiguous memory allocation, arrays have better cache performance.
- Use Cases:
- Suitable for scenarios where the size of the data set is known in advance and frequent random access is required.
- Structure:
-
Linked Lists
- Structure:
- Dynamic Size: Linked lists can grow and shrink dynamically as elements are added or removed.
- Non-Contiguous Memory: Elements (nodes) are stored in non-contiguous memory locations, each node contains data and a reference (or pointer) to the next node.
- Access Time:
- Sequential Access: Linked lists require O(n) time complexity for accessing elements, as traversal from the head node is necessary. = Insertion and Deletion:
- Efficient Operations: Inserting or deleting elements can be done in O(1) time complexity if the pointer to the node is known.
- Memory Utilization:
- Dynamic Allocation: Memory is allocated as needed, which can be more efficient for growing datasets.
- Cache Performance:
- Poor Cache Locality: Due to non-contiguous memory allocation, linked lists typically have poorer cache performance compared to arrays.
- Use Cases:
- Suitable for scenarios where the size of the data set is not known in advance and frequent insertions and deletions are required.
- Structure:
-
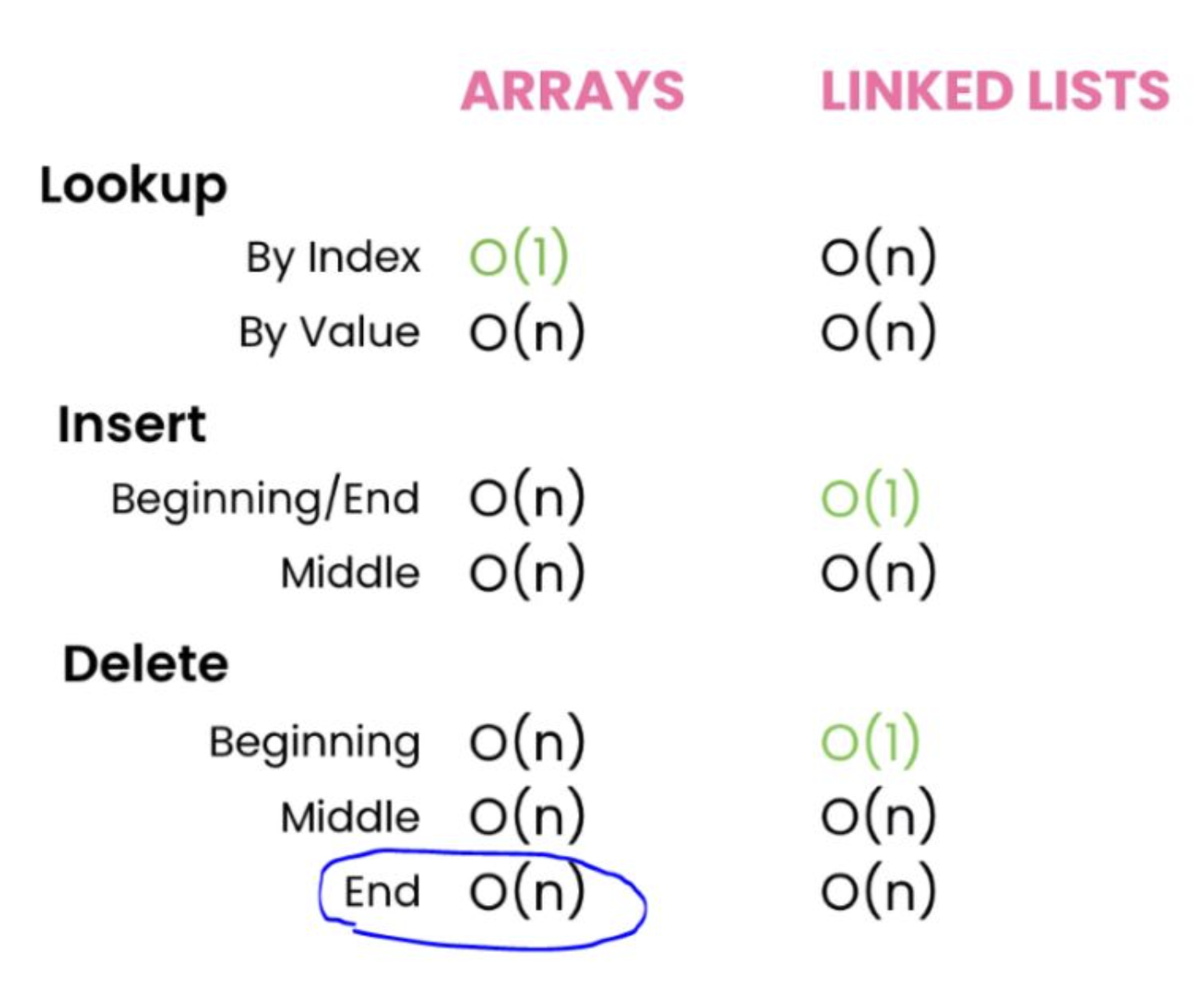
Key Differences
- Memory Allocation:
- Array: Fixed-size, contiguous memory allocation.
- Linked List: Dynamic-size, non-contiguous memory allocation.
- Access Efficiency:
- Array: O(1) access time due to direct indexing.
- Linked List: O(n) access time due to sequential traversal.
- Insertion/Deletion Efficiency:
- Array: O(n) time complexity for arbitrary insertions/deletions.
- Linked List: O(1) time complexity for insertions/deletions if the node pointer is known.
- Memory Overhead:
- Array: No overhead for element storage.
- Linked List: Additional memory overhead for storing pointers in each node.
- Memory Allocation:
-
Summary
- Arrays are best used when fast access to elements is needed and the size of the collection is known and relatively static.
- Linked lists are more flexible with dynamic size and are efficient for frequent insertions and deletions.
- Understanding these differences helps in choosing the appropriate data structure based on the specific requirements of the application.
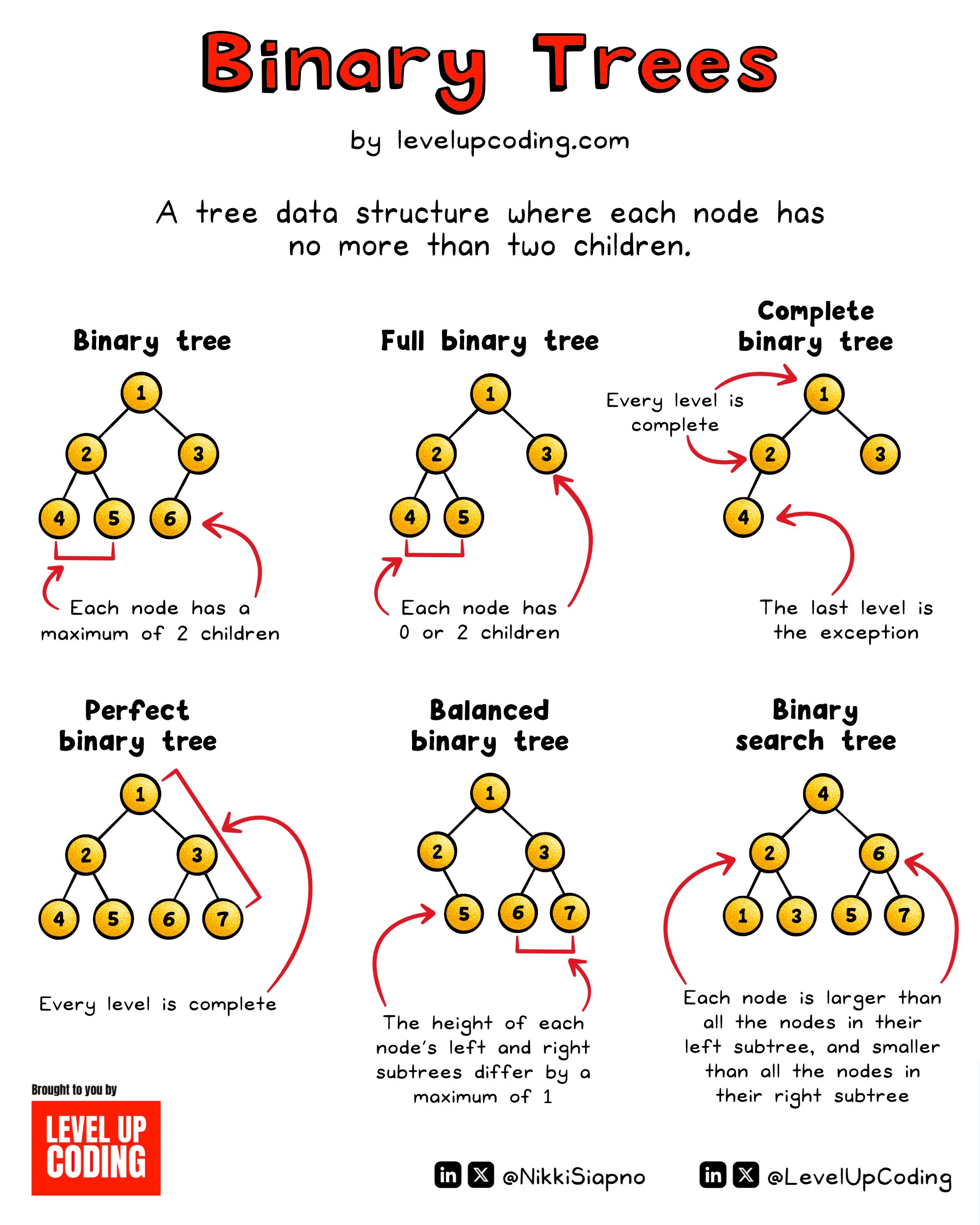
Binary Tress
Breadth-First Search (BFS) and Depth-First Search (DFS)
Imagine you are playing an exploration game in a maze. You want to find your way to the treasure. There are two main ways to explore the maze: BFS and DFS.
BFS (Breadth-First Search)
Think of BFS as if you are exploring the maze layer by layer. First, you look at all the rooms around the room you are in. Then, you go to the next rooms in each direction and do the same thing, and so on. You are expanding your search broadly, layer by layer.
DFS (Depth-First Search)
Think of DFS as if you are exploring the maze by going as deep as you can in one path before going back and trying another. You choose a direction and keep going until you can’t go any further, then you go back and choose another direction, and so on. You are exploring one path deeply before trying another.
Examples in TypeScript
Let’s see how to implement BFS and DFS in TypeScript to explore a maze represented by a graph.
BFS in TypeScript
function bfs(graph: { [key: string]: string[] }, start: string): string[] {
let visited: Set<string> = new Set();
let queue: string[] = [start];
let result: string[] = [];
while (queue.length > 0) {
let node = queue.shift()!;
if (!visited.has(node)) {
visited.add(node);
result.push(node);
queue.push(...graph[node]);
}
}
return result;
}
// Usage example
const graphBFS = {
A: ["B", "C"],
B: ["D", "E"],
C: ["F"],
D: [],
E: ["F"],
F: [],
};
console.log(bfs(graphBFS, "A"));
// Output: ["A", "B", "C", "D", "E", "F"]
DFS in TypeScript
function dfs(graph: { [key: string]: string[] }, start: string): string[] {
let visited: Set<string> = new Set();
let stack: string[] = [start];
let result: string[] = [];
while (stack.length > 0) {
let node = stack.pop()!;
if (!visited.has(node)) {
visited.add(node);
result.push(node);
stack.push(...graph[node]);
}
}
return result;
}
// Usage example
const graphDFS = {
A: ["B", "C"],
B: ["D", "E"],
C: ["F"],
D: [],
E: ["F"],
F: [],
};
console.log(dfs(graphDFS, "A")); // Output: ["A", "C", "F", "B", "E", "D"]
Summary
- BFS (Breadth-First Search): Explores the maze layer by layer, checking all the surrounding rooms before going deeper.
- DFS (Depth-First Search): Explores the maze going as deep as possible in one path before going back and trying another.
In the example:
- BFS: Starts at “A”, then goes to “B” and “C”, and continues exploring layer by layer.
- DFS: Start at “A”, go to “B”, then “D”, and continue exploring as deep as possible on each path before returning.
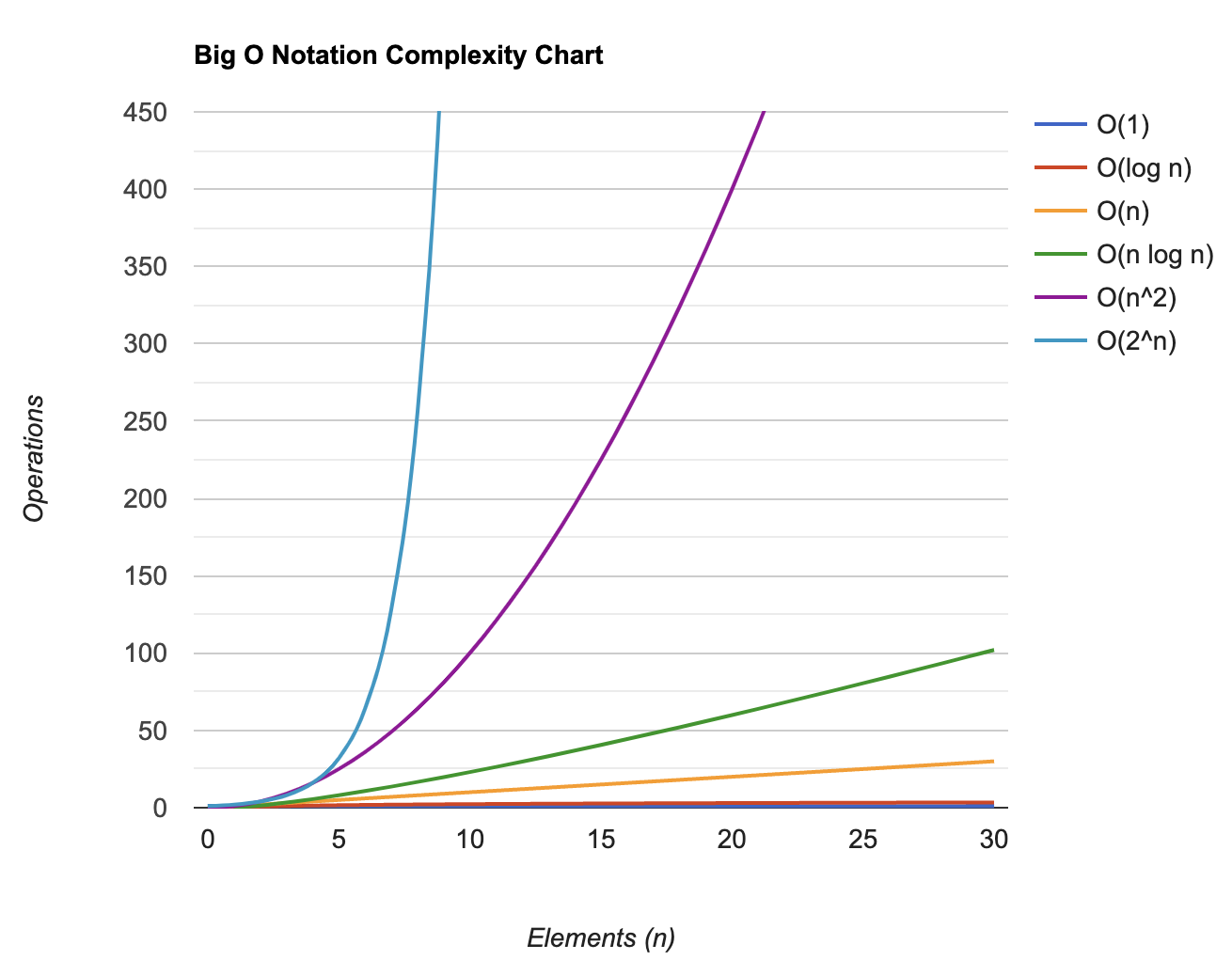
Big O Notation
- O(1) Constant Time
- Best possible case
- If an algorithm has constant time, it means that it will always take the same time to produce the result.
- Example: array.pop() -> removing the last item from an array, regardless of size, will always take the same time!
const accessElementAtIndex = (
arr: number[],
index: number
): number | undefined => {
// Check if index is within bounds of the array
if (index >= 0 && index < arr.length) {
return arr[index]; // Return the element at the specified index
} else {
return undefined; // Return undefined if index is out of bounds
}
};
// Example usage
const array = [2, 5, 8, 12, 16];
const index = 2;
const element = accessElementAtIndex(array, index);
if (element !== undefined) {
console.log(`Element at index ${index}:`, element);
} else {
console.log(`Index ${index} is out of bounds`);
}
- Logarithms O(log n)
- Preferable most of the time
- Logarithms are the inverse of exponentiation.
- Example: Binary search algorithm -> divide and conquer
-
const binarySearch = (arr: number[], target: number): number => {
let left = 0;
let right = arr.length - 1;
while (left <= right) {
const mid = Math.floor((left + right) / 2);
// Check if target is present at mid
if (arr[mid] === target) {
return mid;
}
// If target is greater, ignore left half
if (arr[mid] < target) {
left = mid + 1;
}
// If target is smaller, ignore right half
else {
right = mid - 1;
}
}
// Element is not present in array
return -1;
};
// Example usage
const array = [2, 5, 8, 12, 16, 23, 38, 56, 72, 91];
const target = 72;
const index = binarySearch(array, target);
if (index !== -1) {
console.log(`${target} found at index ${index}`);
} else {
console.log(`${target} not found in the array`);
}
- Linear time O(n)
- Preferable most of the time
- If an algorithm has linear time, it means that the execution time increases linearly according to the size of the input.
- Example: array.forEach() sum of all values
const findMax = (arr: number[]): number | undefined => {
if (arr.length === 0) {
return undefined; // Return undefined if array is empty
}
let max = arr[0]; // Assume the first element is the maximum
// Iterate through the array to find the maximum element
for (let i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i]; // Update max if current element is greater
}
}
return max;
};
// Example usage
const array = [2, 5, 8, 12, 16, 9, 4];
const maxElement = findMax(array);
if (maxElement !== undefined) {
console.log("Maximum element:", maxElement);
} else {
console.log("Array is empty");
}
- Linear Logarithms O(n log n)
- Acceptable
- Examples: Quicksort, Mergesort and Heapsort -> divide and conquer
// Function to merge two sorted arrays
const merge = (left: number[], right: number[]): number[] => {
let result: number[] = [];
let leftIndex = 0;
let rightIndex = 0;
// Merge elements from left and right arrays in sorted order
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
// Concatenate the remaining elements from left or right
return result.concat(left.slice(leftIndex)).concat(right.slice(rightIndex));
};
// Merge Sort function
const mergeSort = (array: number[]): number[] => {
if (array.length <= 1) {
return array;
}
// Divide the array into halves
const mid = Math.floor(array.length / 2);
const left = array.slice(0, mid);
const right = array.slice(mid);
// Recursively sort both halves and merge them
return merge(mergeSort(left), mergeSort(right));
};
// Example usage
const array = [38, 27, 43, 3, 9, 82, 10];
console.log("Original array:", array);
const sortedArray = mergeSort(array);
console.log("Sorted array:", sortedArray);
- Quadratic time O(n²) 💀
- Good to avoid
- The execution time of this algorithm is directly proportional to the square of the input.
- That is:
- n = 2 -> O(4)
- n = 3 -> O(9)
- n = 4 -> O(16)
- n = 5 -> O(25) etc
- Example: Sum of matrices and Bubble Sort
const bubbleSort = (array: number[]): number[] => {
const n = array.length;
// Outer loop for each pass through the array
for (let i = 0; i < n - 1; i++) {
// Inner loop to compare adjacent elements and swap if necessary
for (let j = 0; j < n - 1 - i; j++) {
// Swap elements if they are in the wrong order
if (array[j] > array[j + 1]) {
// Swap array[j] and array[j + 1]
const temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
return array;
};
// Example usage
const array = [38, 27, 43, 3, 9, 82, 10];
console.log("Original array:", array);
const sortedArray = bubbleSort(array);
console.log("Sorted array:", sortedArray);
- Exponential Time O(2^n) 💀💀
- One of the worst cases, it is always good to avoid
- Indicates an algorithm whose growth doubles with each addition to the input data set. The growth curve of an O(2N) function is exponential - starting very shallow and then rising meteorically
- Example: recursive calculation of Fibonacci numbers
- f(0) = 0
- f(1) = 1
- f(n) = f(n - 1) + f(n - 2)
const fibonacci = (n: number): number => {
if (n <= 1) {
return n;
}
return fibonacci(n - 1) + fibonacci(n - 2);
};
// Example usage
const n = 6; // Calculate Fibonacci number at position 6
console.log(`Fibonacci number at position ${n}:`, fibonacci(n));
- Factorial Time O(n!) 💀💀💀
- Worst case possible!
- Always try to avoid!
- Extremely non-performing
- Will execute in factorial time for each operation
- Example: Traveling salesman problem
- “Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?”
// The provided implementation of the traveling salesman algorithm using a brute-force approach has a time complexity of O(n!), where n is the number of points.
// Here's the breakdown:
// Permutations Generation: Generating all possible permutations of the points requires O(n!) time complexity because there are n! permutations for n points.
// Total Distance Calculation: For each permutation, the total distance is calculated, which requires traversing through all points once. This takes O(n) time.
// Finding Shortest Route: After calculating the total distance for each permutation, the shortest route is found by comparing the distances. This takes O(n!) time because there are n! permutations to check.
// Therefore, the overall time complexity of the algorithm is O(n! * n) ≈ O(n!).
// The space complexity mainly comes from storing the permutations and is also O(n!), as it involves storing all possible permutations of the points.
interface Point {
x: number;
y: number;
}
function distance(point1: Point, point2: Point): number {
const dx = point1.x - point2.x;
const dy = point1.y - point2.y;
return Math.sqrt(dx * dx + dy * dy);
}
function permute<T>(arr: T[]): T[][] {
const permutations: T[][] = [];
function generate(current: T[], remaining: T[]): void {
if (remaining.length === 0) {
permutations.push(current);
} else {
for (let i = 0; i < remaining.length; i++) {
const next = current.concat([remaining[i]]);
const rest = [...remaining.slice(0, i), ...remaining.slice(i + 1)];
generate(next, rest);
}
}
}
generate([], arr);
return permutations;
}
function calculateTotalDistance(route: number[], points: Point[]): number {
let totalDistance = 0;
for (let i = 0; i < route.length - 1; i++) {
totalDistance += distance(points[route[i]], points[route[i + 1]]);
}
totalDistance += distance(points[route[route.length - 1]], points[route[0]]);
return totalDistance;
}
function findShortestRoute(points: Point[]): number[] {
const numPoints = points.length;
let shortestDistance = Infinity;
let shortestRoute: number[] = [];
const permutations = permute([...Array(numPoints).keys()]);
for (let i = 0; i < permutations.length; i++) {
const currentDistance = calculateTotalDistance(permutations[i], points);
if (currentDistance < shortestDistance) {
shortestDistance = currentDistance;
shortestRoute = permutations[i];
}
}
return shortestRoute;
}
function generateRandomPoints(
numPoints: number,
minX: number,
maxX: number,
minY: number,
maxY: number
): Point[] {
const points: Point[] = [];
for (let i = 0; i < numPoints; i++) {
const x = Math.floor(Math.random() * (maxX - minX + 1)) + minX;
const y = Math.floor(Math.random() * (maxY - minY + 1)) + minY;
points.push({ x, y });
}
return points;
}
const numPoints = 10,
minX = 0,
maxX = 10,
minY = 0,
maxY = 10;
const points = generateRandomPoints(numPoints, minX, maxX, minY, maxY);
const shortestRoute = findShortestRoute(points);
console.log("Shortest Route:", shortestRoute);
console.log(
"Shortest Distance:",
calculateTotalDistance(shortestRoute, points)
);
- Summary